[Python/LeetCode]코딩테스트 준비를 위한 파이썬 알고리즘 문제 5.Longest Palindromic Substring 참조해설(Medium level)

문제 5. Longest palindromic substring

Given a string s, find the longest palindromic substring in s. You may assume that the maximum length of s is 1000.

Example 1:

Input: "babad" Output: "bab" Note: "aba" is also a valid answer.

Example 2:

Input: "cbbd" Output: "bb"

오늘 해설의 idea는 "Chomolungma" 라는 유저의 글을 참고하였습니다.

 

def longestPalindrome(s):
    #문자열이 공백인 경우 그대로 출력
    if len(s)==0:
    	return s
    
    flag=1
    start=0
    
    #문자열이 공백이 아닌 경우 우측으로 한칸씩 움직이며 회문의 조건을 탐색해 조건의 일치여부에 따라 시작점을 이동
    for i in range(len(s)):
    	if i - 1 >= flag and list(s[i-1-flag:i+1]) == list(reversed(s[i-1-flag:i+1])) :
    		start=i-flag-1
    		flag += 2
    		continue
    	if i >= flag and list(s[i-flag:i+1]) == list(reversed(s[i-flag:i+1])) :
    		start=i-flag
    		flag += 1
            
    return s[start:start+flag]

s = "sdadsbcbaa"

print(longestPalindrome(s))

len(s)==0를 통해 빈 문자열인 경우 그대로 출력시킵니다. 그렇지 않은 경우 for문이 실행됩니다.

 

코드에 써있는 "sdadsbcbaa"를 예를 들어보겠습니다.

i = 0 인 경우

부합하는 if문이 존재하지 않음 => start = 0, flag = 1

i = 1 인 경우

두번째 if문의 첫 번째 조건은 만족하지만, s[0:2] = sd 이기 때문에 두 번째 조건에 부합하지 않음 => start =0, flag = 1

i = 2 인 경우

첫번째 if문의 첫 번째 조건은 만족하지만, s[0:3] = sda 이기 때문에 두 번째 조건에 부합하지 않음

두 번째 if문의 첫 번째 조건을 만족하지만, s[1:3] = da 이기 때문에 두 번째 조건에 부합하지 않음 => start = 0, flag = 1

i = 3인 경우

첫번째 if문의 첫 번째 조건을 만족하고, s[1:4] = dad 이기 때문에 두 번째 조건에 부합 => start = 1, flag = 3

continue에 의해 두번째 if문 통과 안 하고 바로 pass

i = 4인 경우

첫번째 if문의 첫 번째 조건을 만족하고, s[0:5] = sdads 이기 때문에 두 번째 조건에 부합 => start = 0, flag = 5

continue에 의해 두번쨰 if문 통과 안 하고 바로 pass

i = 5인 경우

두번째 if문의 첫 번째 조건을 만족하고, s[0:6] = sdadsb 이기 때문에 두 번째 조건에 부합하지 않음 => start = 0, flag = 5

 

같은 방법으로 끝까지 진행되면 결과적으로 return 값은 s[0:5] 가 되어 sdads 가 출력되게 됩니다.

 

즉, 회문이 좌우대칭 속성을 가지고 있음을 이용하여 검출시점을 기준으로 좌, 우측으로 글자를 이동해가며 검사한 뒤 최종적인 회문을 검출하는 것입니다.

 

 

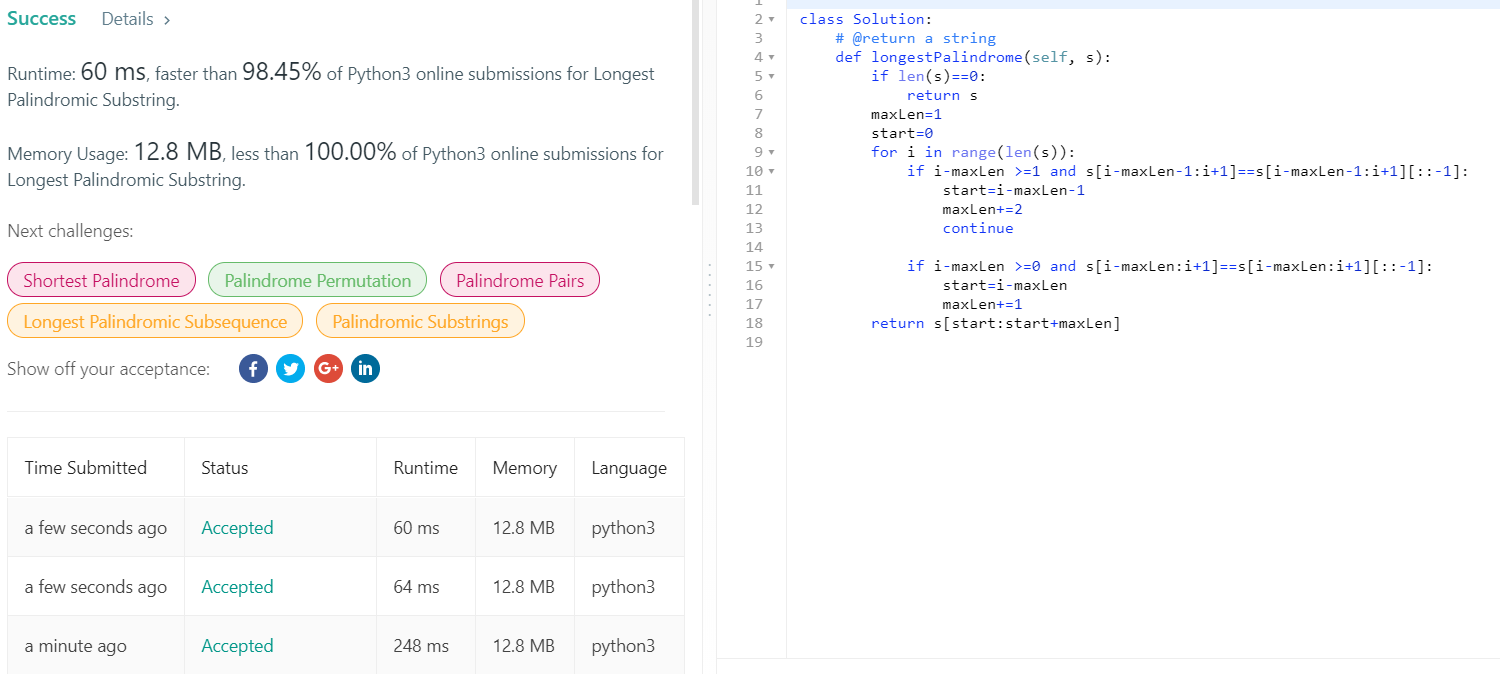
chomolungma의 코드 중 일부 오류가 있어 수정한 뒤 돌렸을 때 결과입니다. 

Runtime이 60ms 로 매우 빠른 것을 알 수 있습니다. 가장 큰 차이는 회문을 검사할 때 reversed를 사용하느냐와 자료형의 특성을 이용하느냐입니다.(사진 속 248ms의 runtime을 가진 accepted가 포스팅된 코드입니다.)

 

참고로 2019년 H사 하반기 공채 코딩 테스트에 회문검출기가 나온 적이 있습니다.

그때 제가 제출한 코드를 조금 손봐서 실행시켜 보았는데, 문자열 길이가 999가 될 때 Runtime 시간 초과가 떠버렸습니다. 관련 내용은 차후에 기회가 되면 포스팅하도록 하겠습니다.

 

https://github.com/Leo-bb/LeetCode/blob/master/My_answer/Prob_5.Longest_Palindromic_Substring.py

Leo-bb/LeetCode