1. 강화 학습이란
인공지능 학습의 방법론인 머신러닝(ML)의 한 계통으로 일반적인 지도 학습과 비지도 학습과는 다른 계통의 학문으로 DP(dymamic programming), MDP(markov decison process)와 같은 개념에 뿌리를 두고 있다.
일반적으로 AI 의 발전은 단순한 계산(computing) 이 아니라 판단(estimation), 의사결정(decison), 창작(creation)을 기계가 행하도록 기대하는 행위인데, 강화 학습은 특히 의사결정(decison)에 집중한다.
- 지도 학습
- 데이터와 레이블의 쌍이 주어지면 기계가 새로운 데이터에 레이블을 붙이는 방법을 학습하는 것
- 즉 문제와 정답을 제공하고, 새로운 문제가 등장하면 "판단"하게 만들고자 함
- 대부분의 회귀모델 CNN과 같은 방법이 여기 속함
- 비지도 학습
- 레이블 없이 데이터만 주어졌을 때 이를 분류하거나 밀도를 추정하도록 학습하는 것
- 즉 데이터의 특징을 분류하고 요약하여 새로운 가치를 생산하도록 기대함
- PCA, 임베딩, 클러스터링 알고리즘 등이 여기 속함
- 강화 학습
- 행동에 대한 보상을 주고 어떠한 상태에서의 행동을 결정하도록 학습하여 최선의 행동을 결정하도록 학습하는 것
2. 동적 계획법(DP)
- 큰 문제를 작은 문제로 세분화하여 문제를 해결하는 방법론
- 세분화된 작은 문제가 "반복적으로 발생" 하며 그에 대한 "답이 항상 같아야 함"
- 즉 세분화된 문제를 1회만 해결하여 답을 기억하고 문제 해결 과정에서 세분화된 문제가 나타날 때는 이미 저장해둔 답을 사용하여 효율을 높이는 방식
- CS 측면에서 메모리와 연산 효율 증가에 큰 도움이 된다.
3. 마르코프 결정 과정(MDP)
- 의사결정자(agent)의 의사결정을 아래 5가지의 인자를 통해 모델링한 방법
- 현재 상태(Status)
- 각 상태에서 취할 수 있는 행동(Action)
- 각 상태에서 취한 행동으로 인해 다음 상태로 넘어갈 확률(Probability)
- 다른 상태로 전이되면서 얻게 되는 보상의 기댓값(Reward)
- 현재 얻는 보상과 미래에 얻을 보상의 관계에 따른 할인율(discount factor)
- 마르코프 결정 과정 풀이를 위해서는 다음 상태로 전이될 확률은 오로지 현재 상태만이 영향을 미친다(즉 이전의 모든 상태와 독립적이다)는 마르코프 특성을 만족해야 한다.

3.1. 모델링
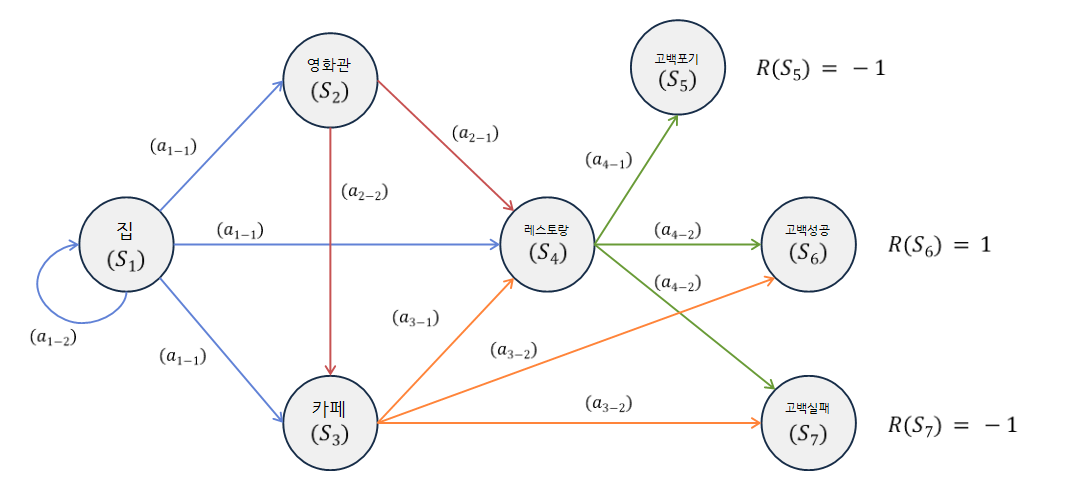
마르코프 결정 과정을 이해하기 위해 분석가 A 씨가 좋아하는 이성 B에게 고백하기 위해 흔하디 흔한 데이트 코스를 짜고 있는 모습을 관찰하며 분석가 A의 고백 계획을 시뮬레이션해보자.
여기서 행동의 주체인 분석가 A 씨를 에이전트(agent)라고 한다.
최초에 에이전트는 본인 집에 있다.($S_1$) 이 상태에서는 에이전트가 데이트 신청을 하는 행동($a_{1-1}$)과 데이트 신청을 포기하는 행동($a_{1-2}$)을 갖는다.
데이트 신청을 하는 행동($a_{1-1}$)을 취했을 때 에이전트는 영화를 보러 가는 상태($S_2$), 저녁을 함께하는 상태($S_4$), 카페에서 얘기를 나누는 상태($S_3$) 를 선택할 수 있다. 이때 각 상태로 전이되는 확률을 $P(S_1, S_2)$, $P(S_1, S_4)$, $P(S_1, S_3)$ 로 표현할 수 있고 확률의 합은 1이 된다.
여러 선택 과정을 거쳐 에이전트가 고백을 하여 성공한 상태($S_6$) 의 보상 $R(S_6) = 1$이고, 실패한 상태($S_7$) 의 보상은 $R(S_7) = -1$ 이 된다. 고백과 무관한 다른 상태의 보상은 0으로 표현할 수 있다.
현실에서는 데이트가 실패했다고 과거로 시간을 돌릴 수 없기 때문에 에이전트는 고백에 성공할 수 있는 데이트 코스(보상이 최대가 되는 최적의 행동 순서)를 찾기 위해 데이트 과정을 반복해서 상상한다. 이 상상 한 번이 곧 한 번의 에피소드 수행이 된다.
최적의 행동 순서를 갖는 에피소드를 찾는 과정에서 보상의 총합이 발산하는 경우가 있을 수 있다. 때문에 시간에 따른 할인 개념($\gamma$)이 필요하다. $\gamma$ 는 0~1 사이의 값을 채택하며 1에 가까울수록 미래 보상을 더 중요하게 평가한다고 볼 수 있다. (보통 0.9 이상으로 설정한다.)
3.2. 이득(return)과 가치(value)
문제를 마르코프 결정 과정의 기본 요소로 모델링하게 되면 주어진 상태에서 미래에 얻을 수 있는 보상의 총합. 즉 이익을 계산할 수 있다.
이익은 모든 행동이 일어났다고 생각하고 현재에서부터 과거로 돌아가며 보상을 더하는 것과 같기 때문에 수식으로 표현하면 아래와 같다.
$$G_n = \sum_{k=0}^\inf \gamma^k R(S_n+k+1)
$$
이익의 개념을 확장해서 특정 상태에서 지나갈 수 있는 전체 경로의 평균과 이익의 기댓값을 구할 수 있다면 그 값을 특정 상태에서 미래에 얻을 수 있는 보상의 총합이라고 할 수 있다. 이를 가치 함수라 하며 아래와 같이 표현할 수 있다.
$$V(s) = E[G_n|S_n=s]
$$
다시 분석가 A 씨 고백 계획으로 돌아가 보자.
최종 상태인 포기($S_5$), 성공($S_6$), 실패($S_7$) 의 가치는 항상 해당 상태의 보상과 같다. 만약 카페($S_3$) 에서 고백하는 행동($a_{3-2}$)이 일어날 때 가치를 구한다면 $\gamma * (1 * P(S_3,S_6) + (-1) * P(S_3,S_7))$ 이 된다.
이렇게 현재 상태의 가치를 계산하기 위해서는 반드시 다음 상태의 가치를 알아야 한다. 때문에 어떤 상태의 가치를 알기 위해서는 최종 상태까지 계산을 반복해야 한다.
이것을 수식화 하면 아래와 같이 표현할 수 있으며 벨만 방정식이라 부르며, 각 상태의 가치를 알기 위해서 모든 상태 S에 대해 $Vn(s) - Vn-1(s) = 0$ 이 될 때까지 반복하여 가치 함수를 산출하는 작업을 가치 반복법이라 한다.
$$V(s) = R(s) + V(s^)
$$
문제가 복잡해질수록 가치 함수의 갱신이 빈번하기 때문에 갱신 값의 차이가 일정 임계치 안에 들어오면 반복을 종료하도록 구현하기도 한다.
정책(policy)
각 상태의 가치를 모두 계산하고 나면 비로소 미래 보상을 최대화하는 행동을 선택할 수 있게 된다. 이는 곧 상태를 입력받으면 최적의 행동을 출력하는 함수로 볼 수 있으며 이 것을 정책($\pi$)이라고 한다.
강화 학습의 목표는 기계가 각 상황에 대해 최선의 선택을 하도록 하는 것이므로 정책의 성능을 극대화하는 것이 곧 강화 학습의 목표라고 볼 수 있다.
가치 반복법에 의해 수렴된 최적의 가치 함수 $V\pi(s)$ 를 알고 있을 때 최적의 정책 함수를 찾는 문제는 현 상태를 입력받아 다음 상태의 가치 함수가 극대화되는 행동을 찾는 문제로 단순화된다.
$$ \pi(s) = \gamma * \sum_{s^{\prime}} p(s,a) * V\pi(s^{\prime})
$$
최적의 정책 함수를 찾기 위해 가치 함수를 계속 업데이트하는 것($V\pi(s)$를 찾는 것) 이 아니라 정책 함수 자체를 업데이트하는 것 도 방법이 될 수 있다.
정책 $\pi(s)$ 가 주어진다면 에이전트가 어떤 상태에 어떤 행동을 하는지 정해져 있다는 것이므로 정책이 쓰일 때마다 모든 상태의 가치 함수를 계산할 필요 없이 $\pi(s)$ 에 의해 발생한 이익의 기댓값만 계산해도 된다. 이렇게 정책 함수에 의해 결정된 가치 함수를 구하는 것을 정책 평가(evaluation) 라 한다.
정책을 평가하면 $\pi(s)$ 를 따랐을 때 와 따르지 않았을 때의 가치의 기댓값을 비교할 수 있는데 이를 통해 가치가 더 큰 방향으로 정책을 수정하는 것을 정책 개선(improvement)라고 한다.
정책은 최초에 무작위로 초기화되고 정책의 평가 - 개선이 반복되면서 점차 강화된다. 이렇게 평가와 개선을 무한히 반복하다 보면 가치 함수와 정책 함수 모두가 변화하지 않는 시점. 즉 수렴하여 정책 함수가 최적화된 시점이 오는데 이러한 작업을 정책 반복법이라고 한다.
정책 반복법은 가치 반복법에 비해 알고리즘도 복잡하고 반복문 하나가 더 추가되기 때문에 수행 과정도 더 길다. (가치 반복법은 정책 반복법 중 정책 평가 과정에서 최댓값을 고르는 과정으로 볼 수 있다.) 단 언제나 가치 반복법이 최적의 정책 함수를 찾는 더 빠른 방법이라고 할 수는 없다.
1) Do-it 강화 학습 입문
2) 위키피디아